마지막으로 분류를 위해 AdaBoost 알고리즘을 조사했습니다. 이 장에서는 AdaBoost가 회귀에 적용하는 알고리즘을 살펴보겠습니다.
AdaBoost 분류기 요약 ↓
https://footprints-toward-data-analysis.11
(부스팅) AdaBoost 분류기
대표적인 부스팅 알고리즘인 AdaBoost 알고리즘을 살펴보자. AdaBoost는 분류 및 회귀 문제 모두에 사용할 수 있는 앙상블 모델입니다. 1. AdaBoost 클래스
Footprints-toward-data-analysis.tistory.com
1. AdaBoost 회귀 알고리즘
2. 간단한 예
3. Sklearn AdaBoost 회귀자 비교
1. AdaBoost 회귀 알고리즘
분류와 마찬가지로 회귀도 매번 데이터의 가중치를 변경하여 약한 학습자를 학습합니다. 이때 분류기는 잘못 분류된 데이터의 가중치를 높이고 잘 분류된 데이터의 가중치를 줄입니다. 이를 통해 다음 약한 학습자는 예측하기 어려운 데이터에 집중할 수 있습니다.
AdaBoost 회귀 알고리즘은 다음과 같습니다.

* 약한 학습자
일반적으로 의사결정 트리 회귀자(max_depth = 3)를 사용하며, 선형 회귀 또는 서포트 벡터 회귀도 사용할 수 있습니다.
2. 간단한 예
예를 들어 AdaBoost 회귀 알고리즘을 이해해 봅시다. 아래 그림과 같이 50개의 시뮬레이션 데이터가 생성되었습니다.
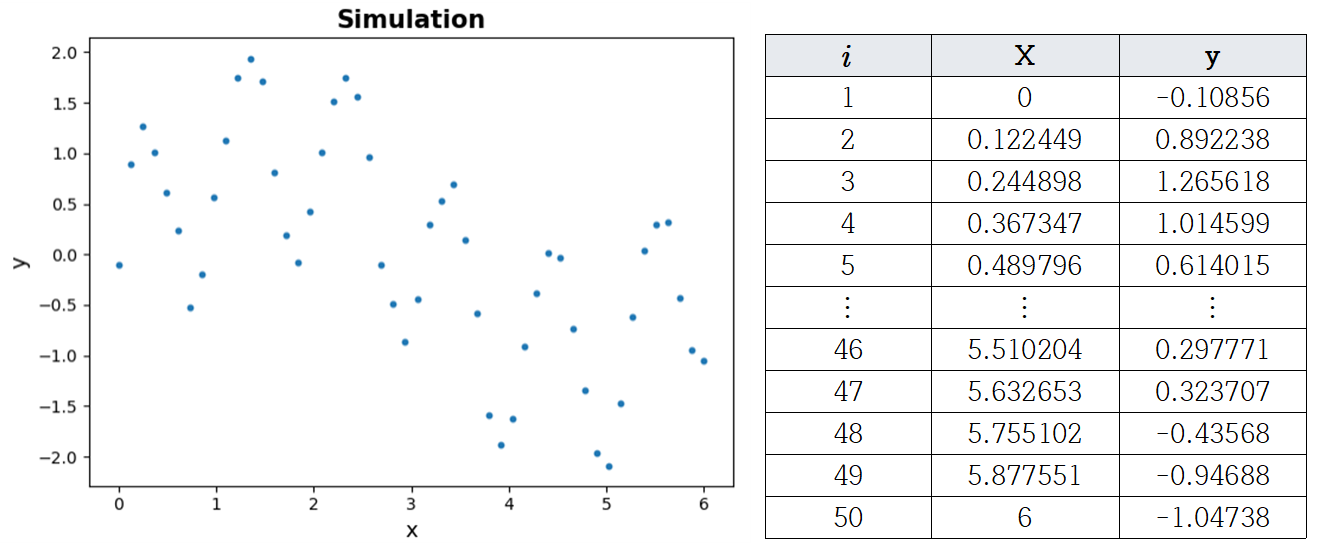
– $t = 1$
50개 레코드의 경우 초기 가중치는 모두 $w_1(i) = \frac{1}{50} = 0.02, i = 1, \cdots, 50$와 같이 설정됩니다.
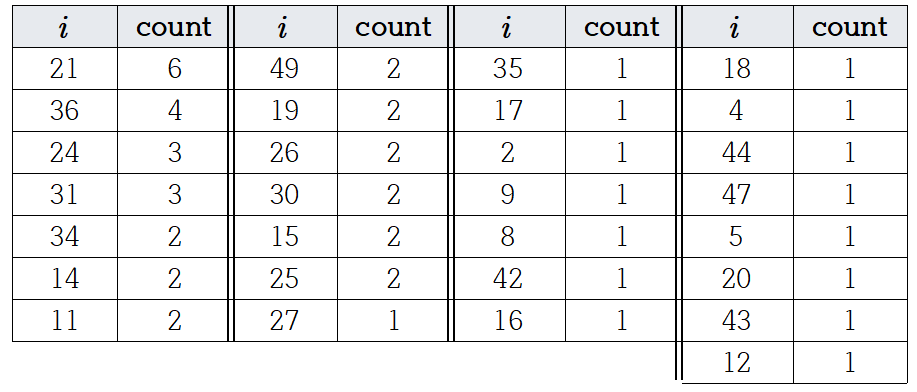
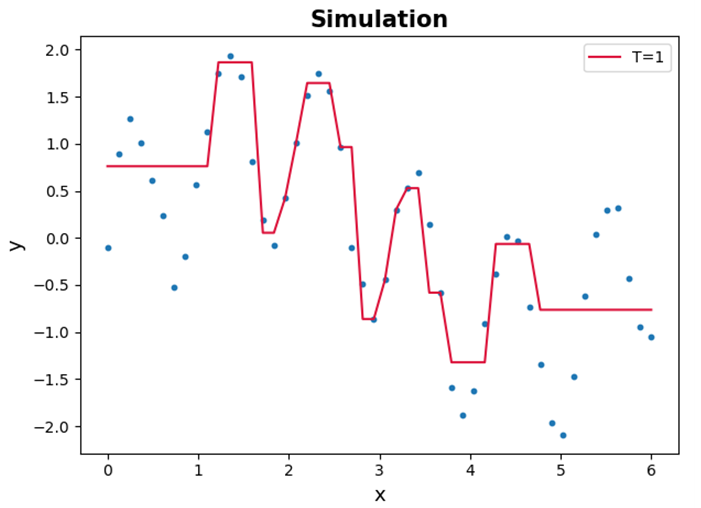
설정된 가중치 $w_1(i)$를 이용하여 훈련 데이터와 동일한 크기의 샘플 데이터 50개를 선택한다. 우리는 이것을 회귀 모델 훈련에 사용합니다. 전체 학습 데이터에 대한 예측비교. 이 시점에서 회귀 모델로 Decision Tree Regressor(max_depth = 4)를 사용했습니다.
생성된 예측값을 사용하여 모든 데이터에 대한 손실을 계산합니다. 이때 $D_{t}$로 인한 손실 가치 $L_{t}^{(i)}$는 $0 \leq L_{t}^{(i) } \leq 1$입니다. 아래 차트에서 예측값과 실제값의 차의 절댓값을 0과 1 사이의 값으로 변환하여 손실값을 계산했음을 알 수 있습니다.
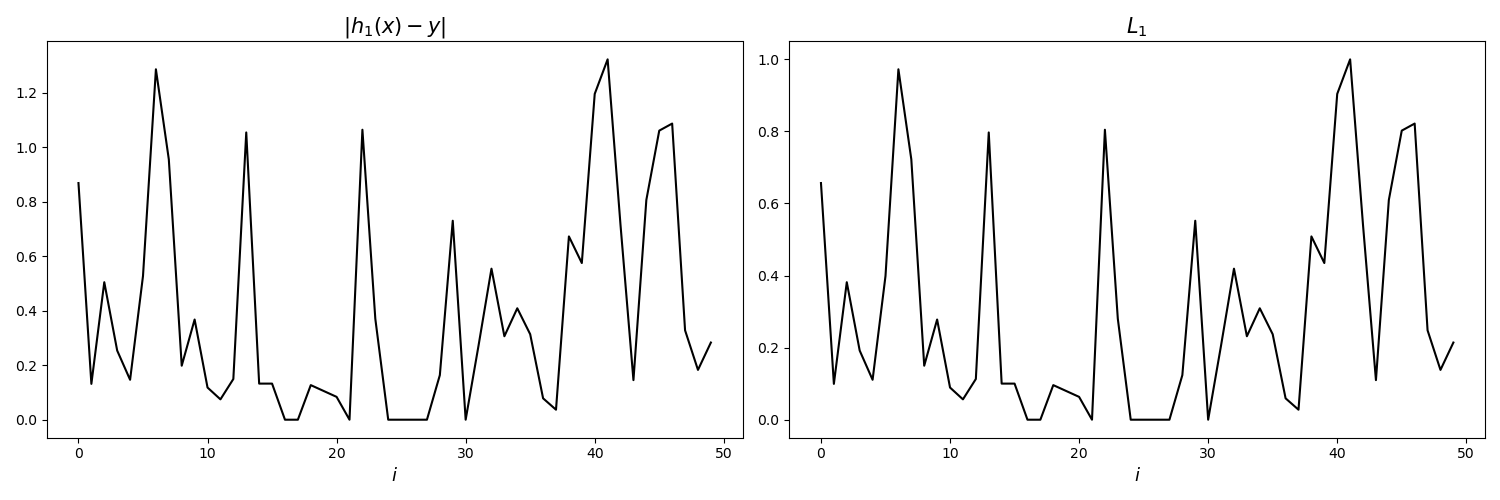
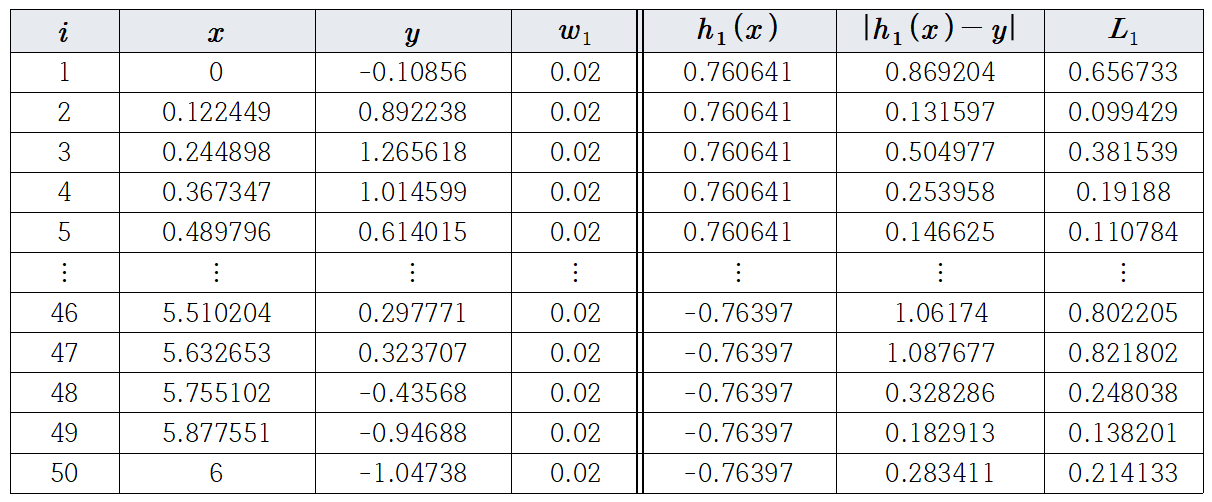
이것으로부터 이제 평균 손실 $\bar{L}_{1}$ 및 $\beta_{1}$를 계산합니다.
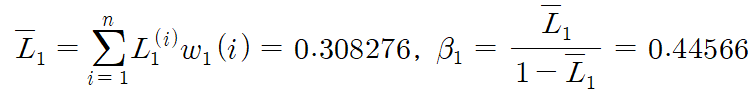
손실이 큰 예에는 상대적으로 큰 가중치를, 손실이 작은 예에는 상대적으로 작은 가중치를 할당하여 가중치를 업데이트합니다. 이런 이유로, 예제 데이터 $D_{2}$를 생성할 때 손실이 큰 예제를 더 많이 선택할 수 있습니다.
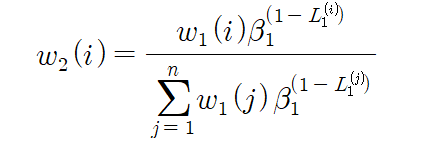
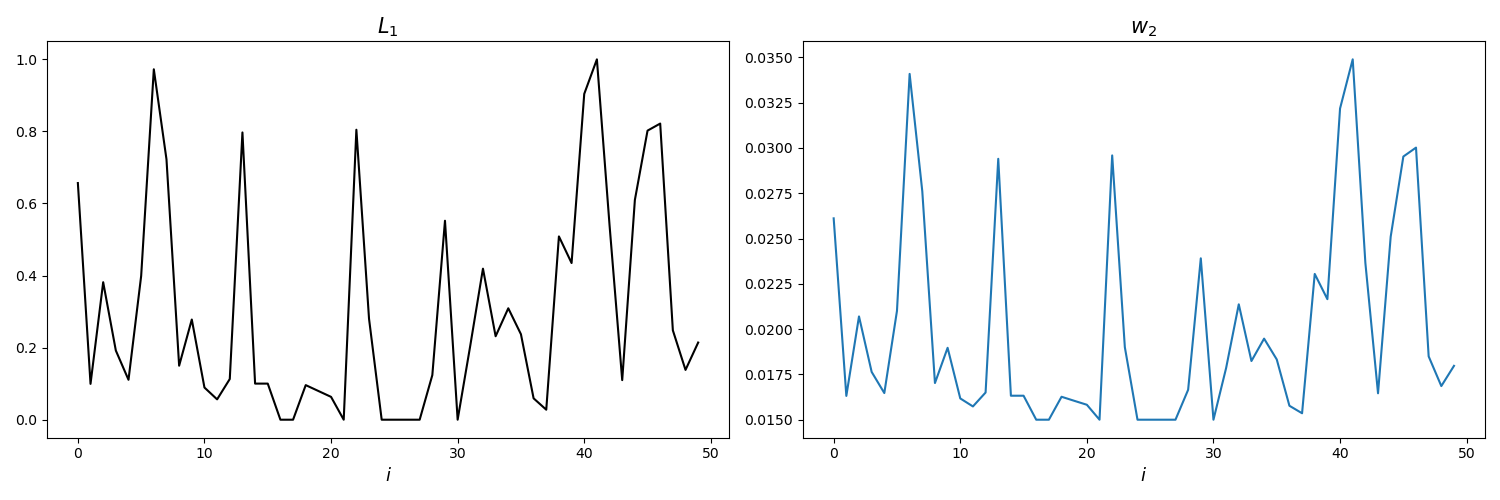
위의 그림에서 손실 분포에 따라 가중치가 부여됨을 알 수 있습니다.
이 과정을 총 10번 반복하면 10개의 회귀 모델이 생성된다. 같은 문제이므로 생략하고 결합하여 예측하는 방법에 대해 자세히 알아보겠습니다.
– 3단계. 모든 테스트 데이터에 대해 예측이 생성되고 가중 중앙값으로 계산됩니다.
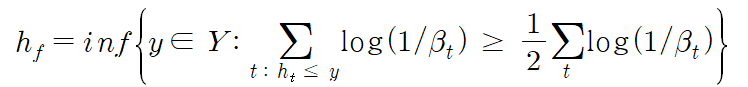
위의 수식으로는 이해하기가 조금 어려우니 예제를 통해 정리해보도록 하겠습니다.
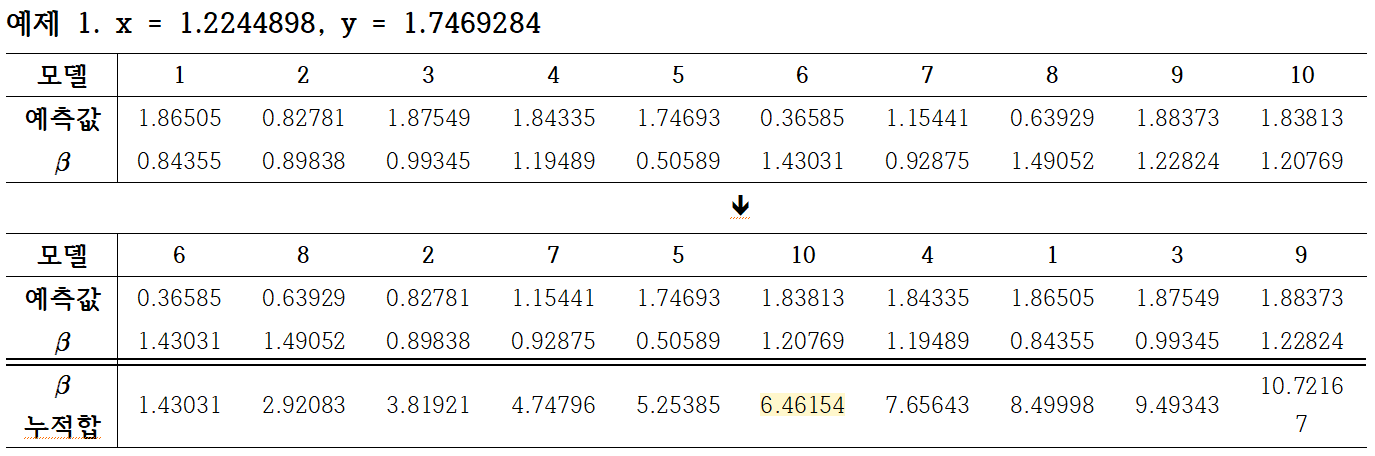
(x, y) = (1.2244898, 1.7469284)로 주어진다고 가정합니다. 그런 다음 처음 10개의 회귀자를 사용하여 예측값을 생성합니다. 생성된 예측값 10개를 작은 것부터 작은 것 순으로 나열합니다. 최종 예측에서는 훈련을 통해 각 모델에 대해 얻은 가중치 $\beta$를 사용합니다!! $\frac{1}{2}\sum_{t=1}^{10}\beta$를 계산한 후 누적합이 처음 증가하는 지점이 가중 중앙값이다. 이것을 사용하여 확실한 예측을 하십시오.
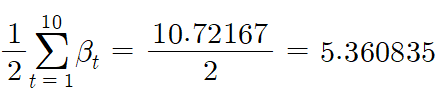
즉 $\beta$의 누적합이 5.360835보다 큰 모델은 10, 4, 1, 3, 9이다. 그 중 처음으로 누적합이 5.360835보다 커지는 시점이 10번째 모델이며, 따라서 이 모델의 예측 값으로 최종 예측이 이루어집니다.
→ (x, y)의 예측값 = (1.2244898, 1.7469284): 1.83813
3. Sklearn AdaBoost 회귀자 비교
제가 직접 만든 AdaBoost 회귀 모델(손)과 sklearn의 AdaBoostRegressor를 비교하려고 합니다.
트리의 깊이를 4로 설정하고 생성할 트리의 총 개수를 10으로 설정한 경우 결과는 다음과 같습니다.
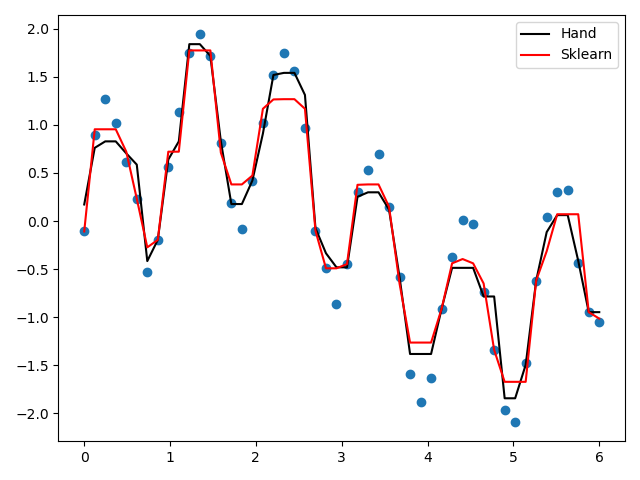
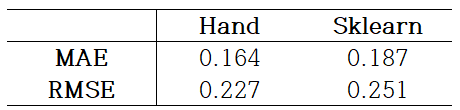
결과적으로 두 모델 모두 데이터 분포를 잘 따르고 있음을 알 수 있다. 특히 MAE와 RMSE 측면에서 Hand가 Sklearn보다 좋은 성능을 보임을 알 수 있다.
AdaBoost Regressor 교육 및 성능 비교 코드 ↓
import numpy as np
from sklearn.ensemble import AdaBoostRegressor
from sklearn.tree import DecisionTreeRegressor
import matplotlib.pyplot as plt
from sklearn.metrics import mean_absolute_error, mean_squared_error
import pandas as pd
from collections import Counter
'''
AdaBoost 훈련
'''
# 데이터
rng = np.random.RandomState(123)
X = np.linspace(0, 6, 50)(:, np.newaxis)
y = np.sin(X).ravel()+np.sin(6*X).ravel() + rng.normal(0, 0.1, X.shape(0))
# 트리 개수, 깊이 설정
T, tree_depth = 10, 4
# 가중치 초기화
w = (1/len(y) for i in range(len(X)))
confi_list = ()
model_list = ()
np.random.seed(123)
for i in range(T):
# w 확률에 따라 훈련 데이터로부터 샘플 데이터 인덱스 추출
train_sample_idx = np.random.choice(range(len(y)), size = len(y), replace = True, p = w)
train_sample = X(train_sample_idx)
train_sample_y = y(train_sample_idx)
# 회귀모델 훈련
weak_learner = DecisionTreeRegressor(max_depth = tree_depth).fit(train_sample, train_sample_y)
# 기존 훈련 데이터에 대한 예측값 생성
train_sample_pred = weak_learner.predict(X)
# 관찰 오류 계산
abs_diff = abs(y - train_sample_pred)
D = max(abs_diff)
loss = abs_diff/D
# 모델 오류 계산
mean_loss = np.sum(loss * w)
if mean_loss >= 0.5:
i = i-1
break
# 베타 계산
confidence = mean_loss/(1-mean_loss)
# 가중치 업데이트
w = w * confidence**(1-loss)
w = w/sum(w)
model_list.append(weak_learner)
confi_list.append(np.log(1/(confidence)))
confi_list = np.array(confi_list)
def adaboost_pred (pred, weight):
sort_pred = np.sort(pred, axis = 1)
# 예측값 정렬 순서
sort_idx = np.argsort(pred, axis = 1)
# 예측값의 가중치 정렬
pred_confi = np.array(confi_list)(sort_idx)
total = np.sum(pred_confi, axis = 1)(0)
# 가중 중앙값의 위치 담기
j_idx_list = ()
for i in pred_confi:
sum_j = 0
for j_idx, j in enumerate(i):
sum_j += j
if sum_j >= 0.5 * total:
j_idx_list.append(j_idx)
break
# 가중 중앙값으로 예측
fin_pred_list = (x(xi) for x, xi in zip(sort_pred, j_idx_list))
return fin_pred_list
# 데이터에 대한 각 회귀모델의 예측값
train_pred = np.array((x.predict(X) for x in model_list)).T
# 최종 예측값
hand_train_pred = adaboost_pred(train_pred, confi_list)
'''
Sklearn vs Hand
'''
# sklearn 모델 생성
sk_ada = AdaBoostRegressor(DecisionTreeRegressor(max_depth = tree_depth), n_estimators = T, random_state = 123).fit(X, y)
sk_pred = sk_ada.predict(X)
plt.figure()
plt.scatter(X, y)
plt.plot(X, hand_train_pred, color = "black", label = "Hand")
plt.plot(X, sk_pred, color = "red", label = "Sklearn")
plt.legend()
plt.tight_layout()
print("sklearn", "MAE:", round(mean_absolute_error(y, sk_pred), 3), "RMSE:", round(mean_squared_error(y, sk_pred, squared = False), 3))
print("hand", "MAE:", round(mean_absolute_error(y, hand_train_pred), 3), "RMSE:", round(mean_squared_error(y, hand_train_pred, squared = False), 3))오늘 우리는 AdaBoost를 회귀 문제에 적용하는 방법을 살펴보았습니다. 손실 또는 종료 예측 부분에서의 분류와 약간 다르지만 전체적인 프로세스는 매우 유사합니다. 다음으로 AdaBoost 분류 문제를 실제 데이터에 적용하고 이에 대한 코드를 구성해 보겠습니다.